s
2
k
– дисперсия
k
-той выборки;
d
ik
– отклонение
i
-той варианты
k
-той выборки.
Необходимым условием применения уравнений (1.8) и (1.9) является
отсутствие статистически достоверной разницы между отдельными
значениями
s
2
k
. В простейшем случае сравнение крайних значений
s
2
k
проводят, исходя из величины критерия
F,
которую вычисляют по уравнению
(3.4) и интерпретируют, как указано в разделе 3.
Примечание 1.2
.
Если при измерениях получают логарифмы
искомых вариант, среднее выборки вычисляют как среднее геометрическое,
используя логарифм вариант:
lg
x
g
=
n
x
n
i
∑
1
lg
,
(1.10)
откуда
x
g
=
=
⋅
⋅
⋅
n
n
x
x
x
......
2
1
antilg (lg
x
g
).
(1.11)
Значения
s
2
,
s
и
s
x
в этом случае также рассчитывают, исходя из
логарифмов вариант, и обозначают соответственно через
s
2
lg
,
s
lg
и
s
lg
õ
g
.
Пример 1.1
. При определении содержания стрептоцида в образце
линимента были получены следующие данные:
Содержание в
образце
Номер опыта
i
1
2
3
4
5
x
i
, %
9,52
9,55
9,83
10,12
10,33
n =
5
; f = n
– 1
=
5 – 1
=
4.
x =
n
x
n
i
∑
1
=
5
33
,
10
12
,
10
83
,
9
55
,
9
52
,
9
+
+
+
+
=
9,87
.
d
i
=
87
,
9
−
=
−
i
i
x
x
x
,
т. е.
d
i=1
=
87
,
9
52
,
9
−
= 0,35
и т. д. до
i =
5.
s
2
=
f
d
n
i
∑
1
2
=
f
x
n
x
n
i
∑
−
1
2
2
=
4
87
,
9
5
)
33
,
10
12
,
10
83
,
9
55
,
9
52
,
9
(
2
2
2
2
2
2
⋅
−
+
+
+
+
=
=
0,1252;
s =
2
s
=
1252
,
0
=
0,3538
;
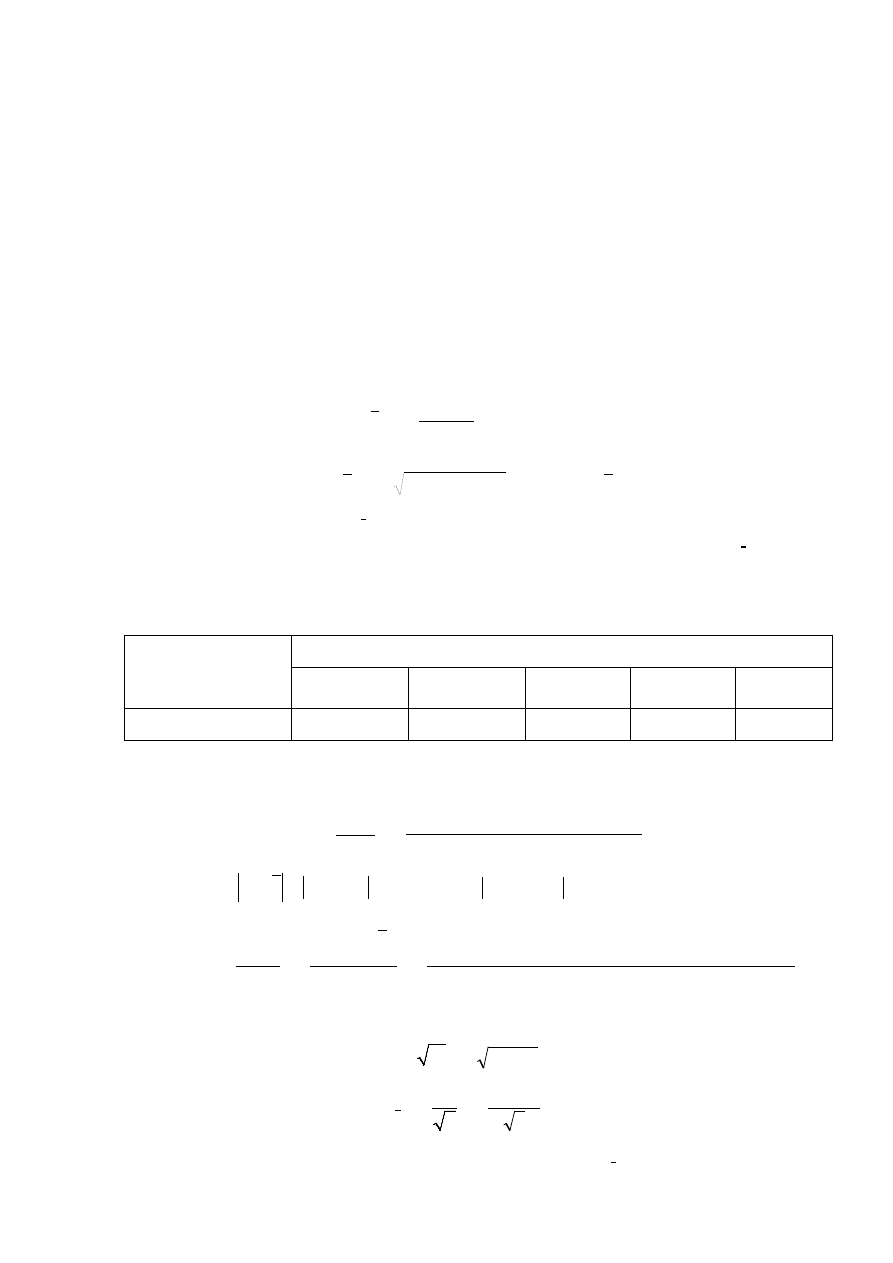
s
x
=
s
n
=
5
3538
,
0
=
0,1582
.
Как было указано выше, значения
х
,
s
2
,
s
и
s
x
могут быть признаны
Предыдущая < | 293 | > Следующая | Главная | pharma-14@mail.ru | pharmacopeia.ru