;
.
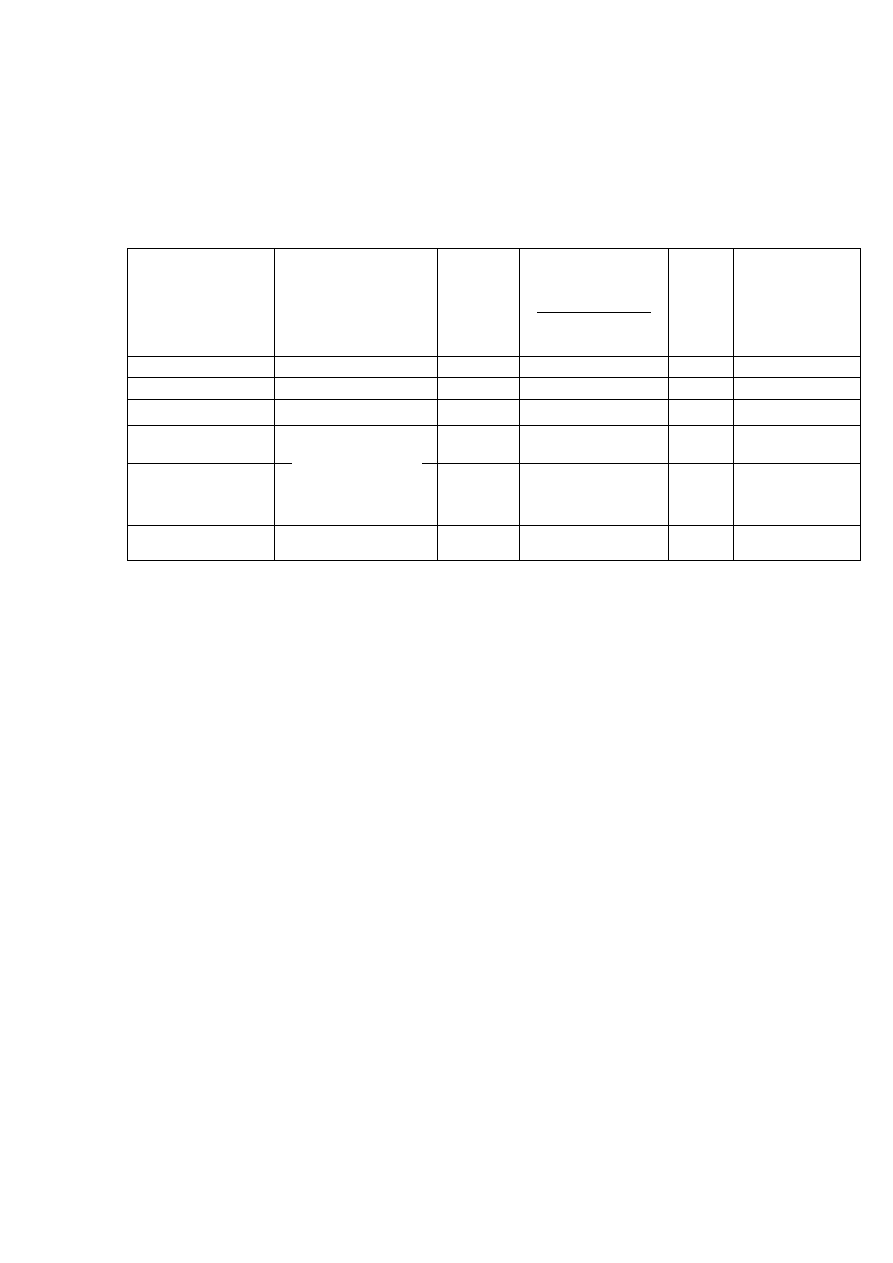
Таблица 3
−
Сводная таблица дисперсионного анализа (двухдозовая
рандомизированная постановка)
Источник
дисперсии
(показатель)
Число
степеней
свободы
(
f)
Сумма
квадратов
Средний квадрат,
Наблюда
емое
значение
критерия
Фишера
F
набл.
Критическое
значение
критерия
Фишера
F
критич.
Препараты
1
0,99
0,99
Регрессия
1
58,44
58,44
292,2 >7,40 (
P=
99 %)
Параллельность
1
0,51
0,51
2,55 <4,11 (
P=
95 %)
Обработки
59,94
19,98
Отклонение
7,29
0,20
Итог
67,23
n
= 10 (число ответов в группе);
N
= 40 (общее число ответов в опыте);
m
= 0 (число утраченных и замененных значений).
Значимость различий дисперсий проверяют с помощью критерия
Фишера. Обязательным является выполнение требований для показателей
«Регрессия»
и
«Параллельность»
. Эти требования заключаются в том, что
для
«Регрессии»
наблюдаемое значение критерия Фишера должно быть
больше критического (
P =
99 %), а для
«Параллельности»
– меньше
критического
(
P =
95 %).
Для того чтобы найти
F
набл.
средние квадраты показателей делят на
средний квадрат показателя
«Отклонение»
. Полученные результаты
сравнивают с табличными критическими значениями критерия Фишера
(приложение, табл. III). Число степеней свободы
f
1
= 1, а
f
2
= 36.
( )
∑
=
−
=
−
=
23
,
67
8
,
124
03
,
192
2
K
y
Итог
29
,
7
94
,
59
23
,
67
=
−
=
−
=
обработки
итог
Отклонение
f
квадратов
сумма
об.
3
1
4
1
f
k
=
=
−
=
−
36
3
39
1
об.
=
−
=
=
−
−
−
m
f
N
39
1
=
−
−
m
N
Предыдущая < | 328 | > Следующая | Главная | pharma-14@mail.ru | pharmacopeia.ru