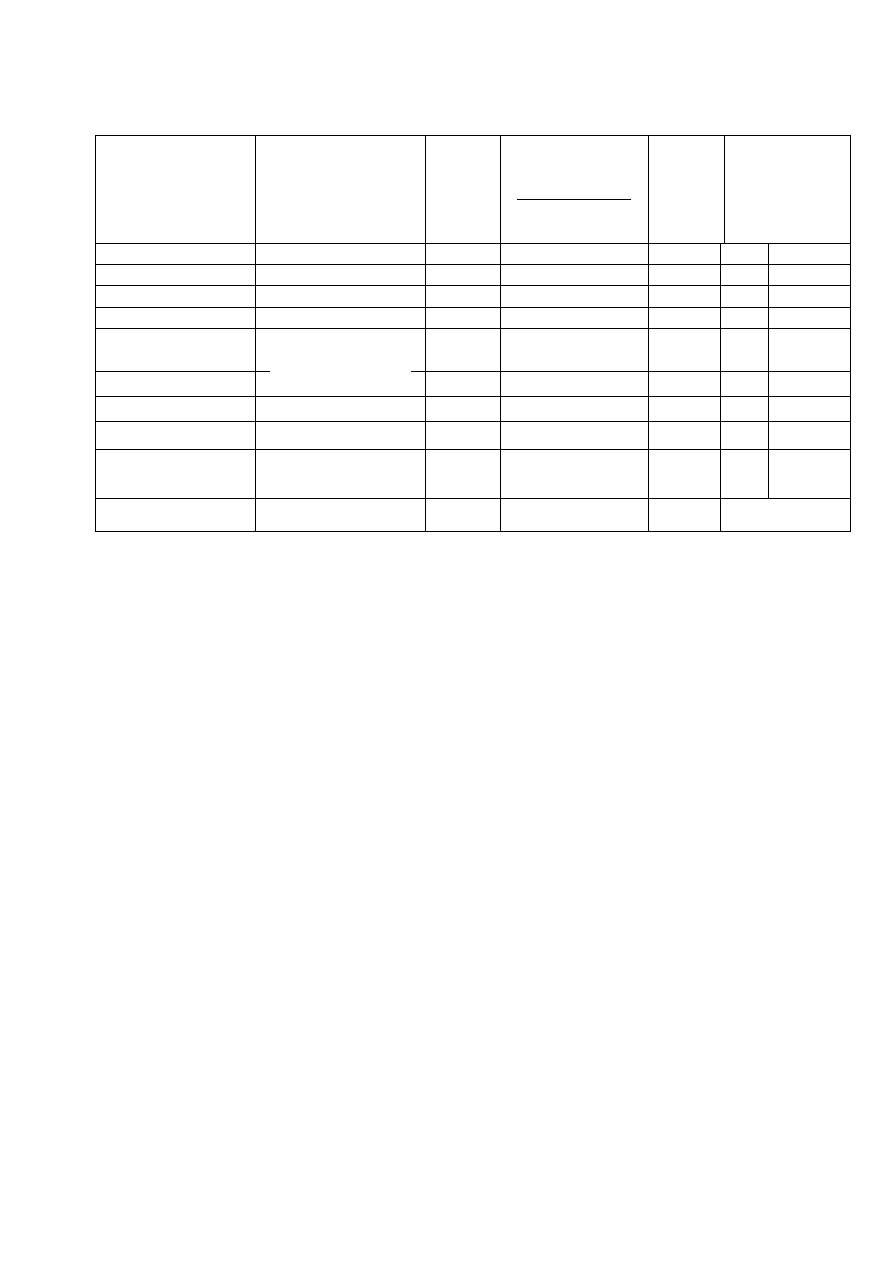
Таблица 17
−
Сводная таблица дисперсионного анализа (трехдозовый
латинский квадрат)
Источник
дисперсии
(показатель)
Число
степеней
свободы
(
f)
Сумма
квадрато
в
Средний квадрат
Наблюдае
мое
значение
критерия
Фишера
F
набл.
Критиче-
ское
значение
критерия
Фишера
F
критич.
Препараты
1
0,401
0,401
4,307
Регрессия
1
26,46
26,46
284,18 >8,1 (
P=
99 %)
Параллельность
1
0,027
0,027
0,290 <4,35 (
P=
95 %)
Квадратичность
1
0,055
0,055
0,591 <4,35 (
P=
95 %)
Разность
квадратичностей
1
0,0361
0,0361
0,3877 <4,35 (
P=
95 %)
Обработки
26,9789
5,39578
Строки
0,2189
0,04378
0,4702 <4,1 (
P=
99 %)
Столбцы
0,2322
0,04644
0,4988 <4,1 (
P=
99 %)
Отклонение
1,8622
0,09311
2
s
=
Итог
29,2922
0,83692
n
= 6 (число ответов на дозу);
N
= 36 (общее число ответов в опыте);
m
= 0 (число утраченных и замененных значений).
Значимость различий дисперсий проверяют с помощью критерия
Фишера. Обязательным является выполнение требований для показателей
«Регрессия»
,
«Параллельность»
,
«Квадратичность»
,
«Разность
квадратичностей»
,
«Строки»
и
«Столбцы»
. Для
«Регрессии»
наблюдаемое
значение критерия Фишера должно быть больше критического (
P =
99 %), а
для показателей
«Параллельность»
(
P =
95 %),
«Строки»
(
P =
99 %) и
«Столбцы»
(
P =
99 %) – меньше критического. Показатель
«Регрессия»
характеризует дозозависимость,
«Параллельность»
–
параллельность двух
линий регрессии,
«Квадратичность»
и
«Разность квадратичностей»
–
линейность
дозозависимости,
а
«Строки»
и
«Столбцы»
–
сбалансированность ответов на протяжении всего опыта.
Для того чтобы найти
F
набл.
средние квадраты показателей делят на
средний квадрат показателя
«Отклонение»
. Полученные результаты
сравнивают с табличными критическими значениями критерия Фишера
(приложение, табл. III). Число степеней свободы
f
1
= 1 или 5, а
f
2
= 20.
f
квадратов
сумма
об.
5
1
6
1
f
k
=
=
−
=
−
стр.
5
1
f
n
=
=
−
ст.
5
1
f
n
=
=
−
20
1
ст.
стр.
об.
=
−
−
−
−
−
−
m
f
f
f
N
35
1
=
−
−
m
N
Предыдущая < | 342 | > Следующая | Главная | pharma-14@mail.ru | pharmacopeia.ru