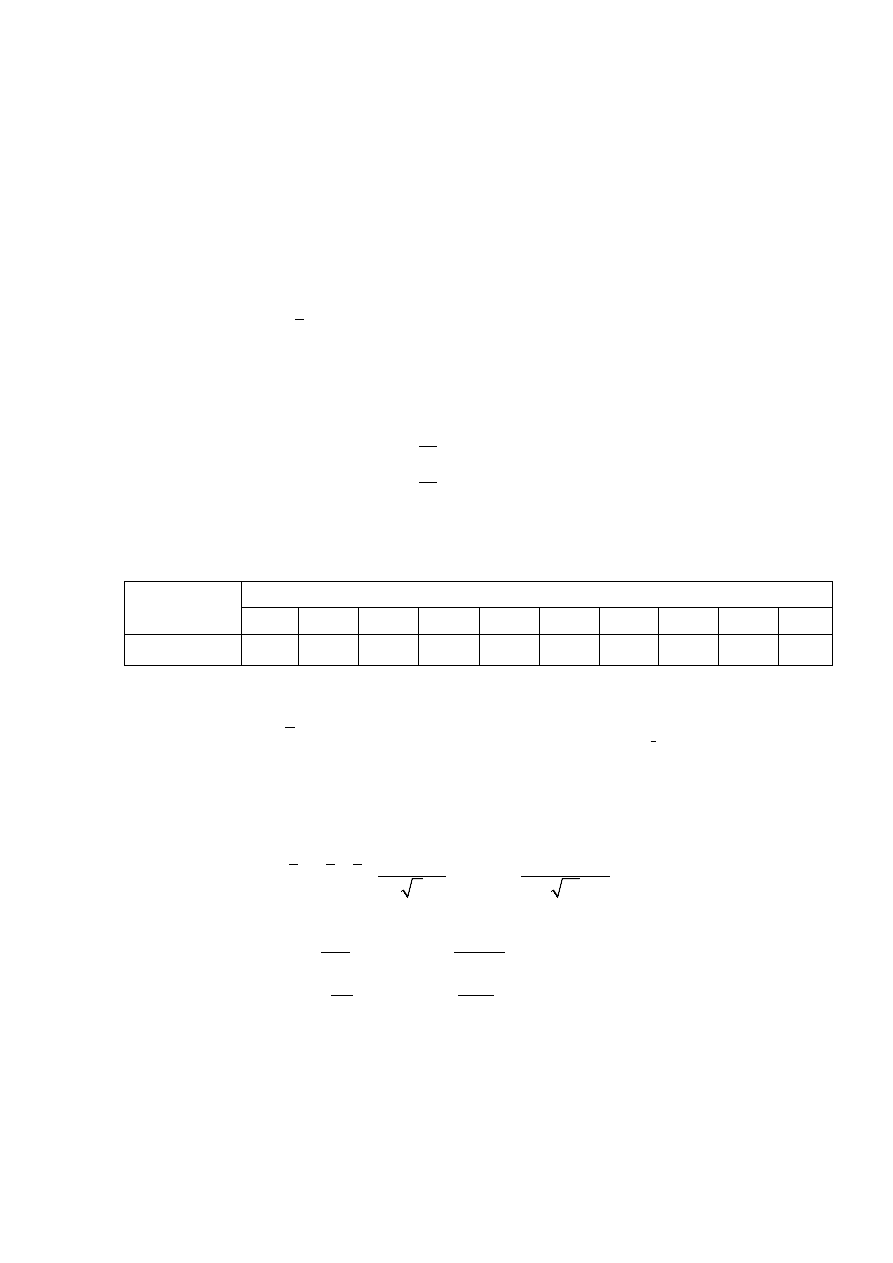
( , )
i
i
x
x x t P f s
± ∆ = ±
⋅
.
(2.4)
Этот интервал является доверительным интервалом результата
единичного определения. Для него с доверительной вероятностью
Р
выполняются взаимосвязанные условия:
x
i
–
x
x
x
i
∆
+
≤
≤
∆
µ
,
(2.5)
x
x
x
i
∆
+
≤
≤
∆
−
µ
µ
.
(2.6)
Значения
x
∆
и
x
∆
из выражений (2.2) и (2.4) используют при
вычислении относительных погрешностей отдельной варианты (ε) и среднего
результата (
ε�
), выражая эти величины в %:
ε
=
∆𝑥
𝑥
∙
100%
, (2.7)
ε�
=
∆𝑥̅
𝑥̅
∙
100%
. (2.8)
Пример 2.1.
В результате определения содержания хинона в
стандартном образце хингидрона были получены следующие данные
(
n
= 10):
Содержание
хинона
Номер опыта
i
1
2
3
4
5
6
7
8
9
10
x
i
, %
49,80 49,83 49,87 49,87 49,92 50,01 50,05 50,06 50,10 50,11
Расчеты по формулам (1.2), (1.4), (1.5), (1.6), (1.9) дали следующие
результаты:
x
= 49,96;
f
= 9;
s
2
= 0,01366;
s
= 0,1169;
s
x
= 0,03696.
Доверительные интервалы результата отдельного определения и
среднего результата при
Р
= 90 % получаем согласно (2.4) и (2.2):
( , )
(90%,9)
1,83 0,1169
0,21
i
i
i
i
i
x
x x t P f s x t
s x
x
± ∆ = ±
⋅ = ±
⋅ = ±
⋅
= ±
;
( , )
1,83 0,1169
49,96
49,96 0,07.
10
t P f s
x
x x
n
⋅
⋅
± ∆ = ±
=
±
=
±
Тогда относительные погрешности
ε
и
ε�
, согласно (2.7) и (2.8), равны:
ε
=
∆
𝑥
𝑥̅
∙
100% =
0,21
49,96
∙
100 % = 0,42 %;
ε�
=
∆
𝑥̅
𝑥̅
∙
100% =
0
,
07
49
,
96
∙
100 % = 0,14 %
.
Обозначая истинное содержание хинона в хингидроне через µ, можно
считать, что с 90 % доверительной вероятностью справедливы неравенства:
μ −
0,21
≤
𝑥
𝑖
≤
μ
+ 0,21
;
𝑥
𝑖
−
0,21
≤
µ
≤
𝑥
𝑖
+ 0,21
(при любом
i);
μ −
0,07
≤
𝑥̅
≤
μ
+ 0,07;
𝑥̅ −
0,07
≤
μ
≤
𝑥̅
+ 0,07
(при
n
= 10).
Примечание 2.2. Вычисление доверительных интервалов для случая,
описанного в примечании 1.2, проводят, исходя из логарифмов вариант.
Предыдущая < | 297 | > Следующая | Главная | pharma-14@mail.ru | pharmacopeia.ru