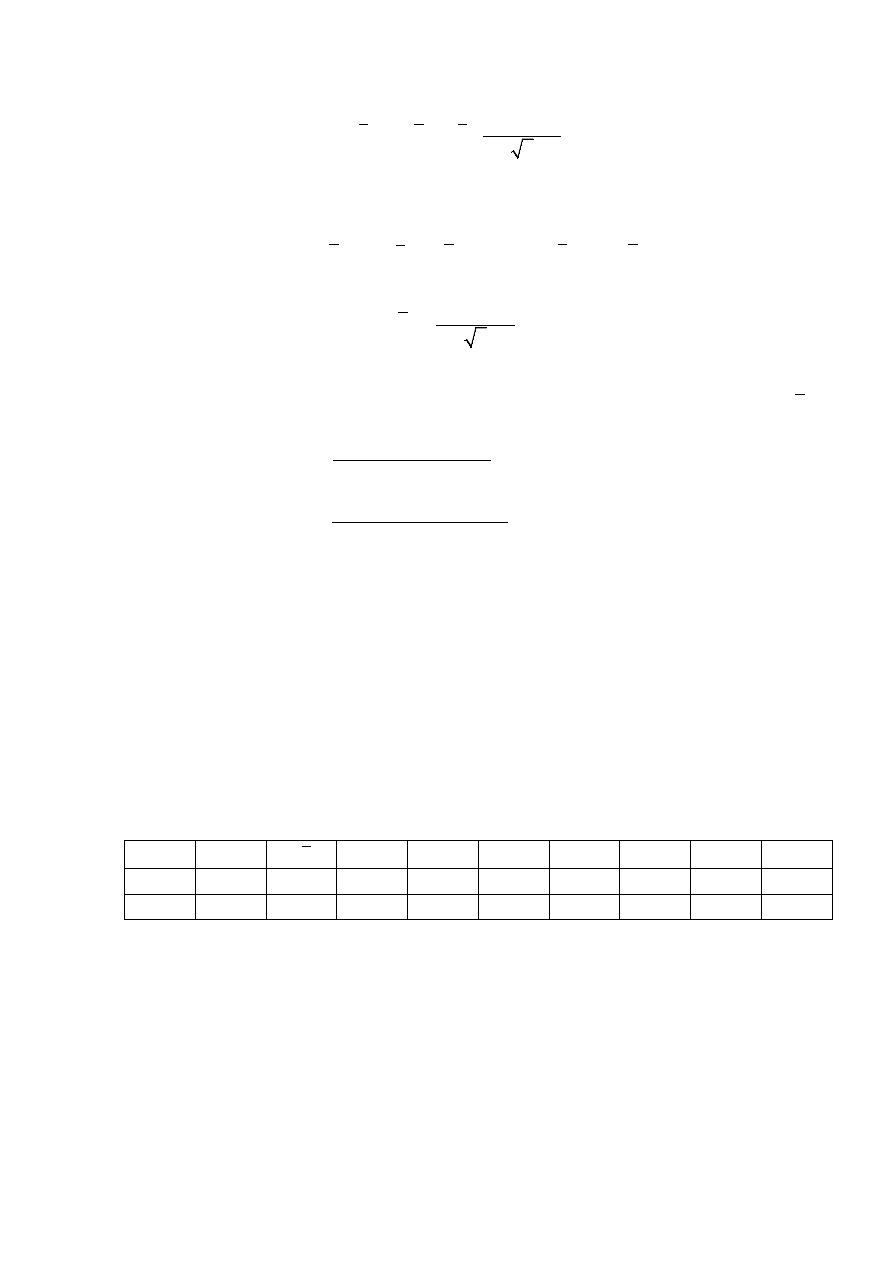
Тогда выражения (2.2) и (2.4) принимают вид:
lg
lg
( , )
lg
lg
t P f s
x
x
x
n
⋅
± ∆
=
±
;
(2.9)
lg
lg
lg
lg
( , )
i
i
x
x
x t P f s
± ∆
=
±
⋅
.
(2.10)
Потенцирование выражений (2.9) и (2.10) приводит к несимметричным
доверительным интервалам для значений
х
и
x
i
.
antilg(lg
x
–
x
lg
∆
)
≤
x
≤
antilg(lg
x
+
∆
lg
x
);
(2.11)
antilg(lg
x
i
–
∆
lg
x
i
)
≤
≤
i
x
antilg(lg
x
i
+
∆
lg
x
i
),
(2.12)
где
∆
lg
x
=
lg
( , )
t p f s
n
⋅
;
∆
lg
x
i
=
⋅
)
,
(
f
P
t
s
lg
.
При этом для нижних и верхних границ доверительных интервалов
x
и
x
имеем:
ε�
=
�
|
antilg
(
lg 𝑥̅
±
∆lg𝑥̅
)
−𝑥̅
|
𝑥̅
�
∙
100 %
; (2.12 a)
ε
=
�
|
antilg
(
lg
𝑥
𝑖
±
∆ lg 𝑥
)
−𝑥
𝑖
|
𝑥
𝑖
�
∙
100 %
. (2.12 б)
3. Метрологическая характеристика метода анализа.
Сравнение двух методов анализа по воспроизводимости.
С целью получения метрологической характеристики метода проводят
совместную статистическую обработку одной или нескольких выборок,
полученных при анализе образцов с известным содержанием определяемого
компонента µ. Результаты статистической обработки представляют в виде
табл. 1.
Таблица 1
−
Метрологические характеристики метода анализа
µ
f
x
s
2
s
Р
T (P, f)
∆
х
ε
δ
1
2
3
4
5
6
7
8
9
10*
*- Графа 10 заполняется в том случае, если реализуется неравенство (3.2).
Примечание 3.1. При проведении совместной статистической
обработки нескольких выборок, полученных при анализе образцов с разным
содержанием определяемого компонента µ, данные в графах 1, 2, 3, 4, 9 и 10
табл. 1 приводят отдельно для каждой выборки. При этом в графах 2, 4, 5, 7,
8 в последней строке под чертой приводят обобщенные значения
f
,
s
2
,
s
,
t
,
∆
х
,
вычисленные с учетом примечания 1.1.
Если для выборки объема
m
величина
|
μ −
x
�
| > 0
, следует решить
вопрос о наличии или отсутствии систематической ошибки. Для этого
Предыдущая < | 298 | > Следующая | Главная | pharma-14@mail.ru | pharmacopeia.ru