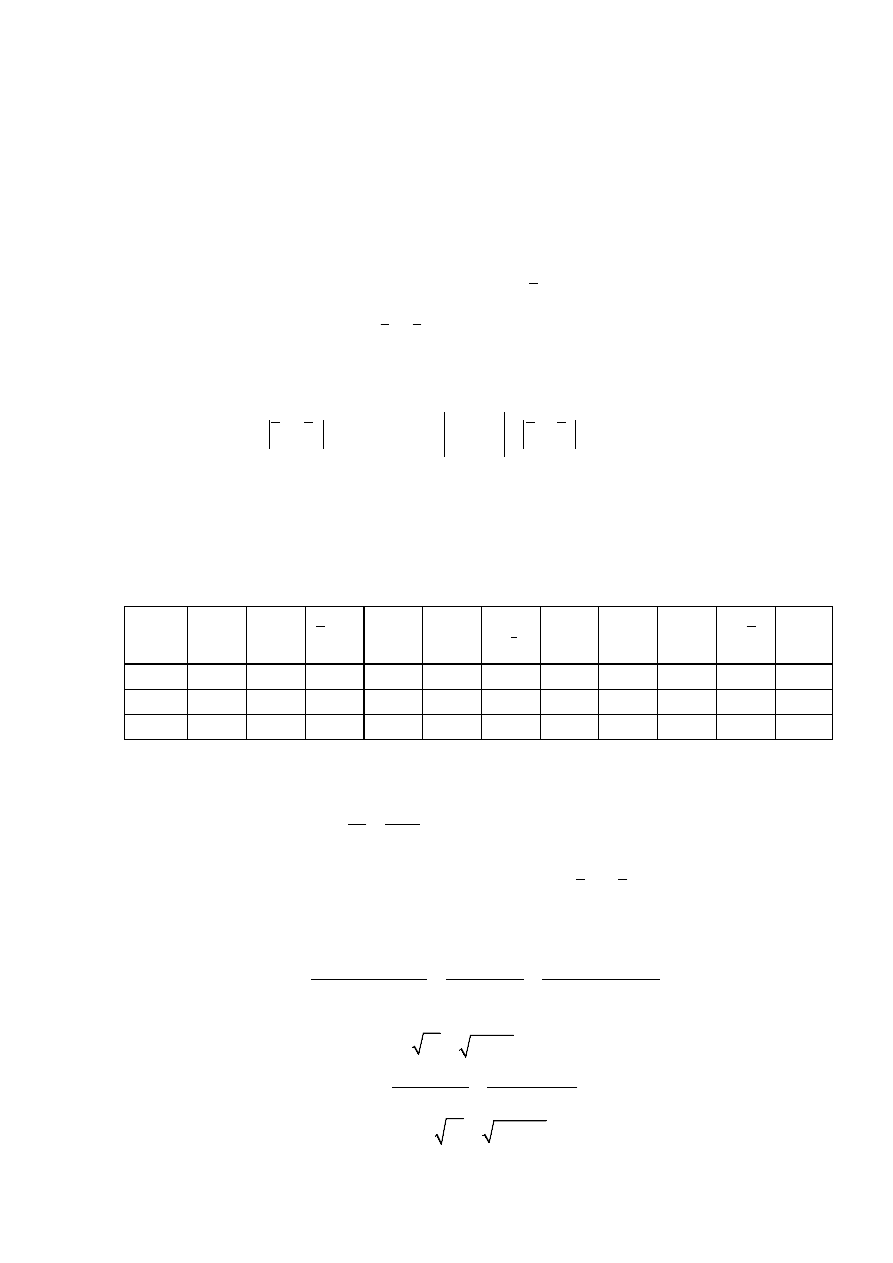
гипотезы:
𝑥̅
1
= µ
(4.3 а) и
𝑥̅
2
= µ
(4.3 б). Проверку выполняют так, как
описано в разделе 3 с помощью выражений (3.1) и (3.2) отдельно для каждой
из гипотез. Если гипотезы (4.3 а) и (4.3 б) статистически достоверны, то
следует признать достоверной и гипотезу (4.3). В противном случае гипотеза
(4.3) должна быть отброшена.
Примечание 4.2. В случае, предусмотренном примечанием 1.2, при
сравнении средних используют величины
2
lg
,
lg
s
x
g
и
lg
s
.
Когда разность (
2
1
x
x
−
) оказывается значимой, определяют
доверительный интервал для разности соответствующих генеральных
средних
1
x
∧
и
2
x
∧
:
2
1
x
x
−
–
t
(
P
,
f
)
1
2
1
2
( , )
P
P
s
x x
t P f s
x x
∧
∧
⋅ ≤
−
≤
−
+
⋅
. (4.10)
Пример 4.1
.
При определении содержания основного вещества в
двух образцах препарата, изготовленных по разной технологии, получены
метрологические характеристики средних результатов, приведенные
в табл. 5.
Таблица 5
−
Полученные данные метрологических характеристик средних
результатов
Номер
образ-
ца
n
f
x
,
%
s
2
s
s
x
Р,%
t
(
P
,
f
)
x
∆
x
∆
ε�
,%
1
2
3
4
5
6
7
8
9
10
11
12
1
8
7 99,10 0,25 0,50 0,18 95 2,36 1,18 0,42 0,42
2
6
5 98,33 0,31 0,56 0,23 95 2,57 1,44 0,59 0,60
Требуется решить, является ли первый образец по данному показателю
лучшим в сравнении со вторым образцом. Поскольку
F
=
2
2
2
1
0,31 1,24
0,25
s
s
=
=
< F
(99 %, 5,7) = 7,46,
то согласно неравенству (3.5 а) статистически достоверное различие величин
2
1
s
и
2
2
s
отсутствует. Следовательно, гипотеза
1
x
=
2
x
(4.3) проверяется с
помощью уравнений (1.7), (1.8), (4.4) и (4.5).
(
)
2
2
2
1
1 1
2 2
1
2
1
1
7 0,25 5 0,31 0,275
7 5
(
1)
k g
k
k
k
k=g
k
k
n
s
f s
f s
s
f
f
n
=
=
=
− ⋅
+
⋅
+ ⋅
=
=
=
=
+
+
−
∑
∑
;
s =
2
0,275 0,524.
s
=
=
2
2
1
2
1
2
(
) 0,275(8 6) 0,0802
8 6
P
s n n
s
n n
+
+
=
=
=
⋅
⋅
;
2
0,0802 0,283.
P
P
s
s
=
=
=
f = n
1
+ n
2
–
2
=
8 + 6 – 2 = 12
.
Предыдущая < | 304 | > Следующая | Главная | pharma-14@mail.ru | pharmacopeia.ru