2
2
1
1
a
x
j
s
s
b n
m
=
+
.
(6.17 а)
С учетом значений
s
y
и
s
x
могут быть найдены значения величин ∆
Y
и
∆
X
:
∆
Y =
s
y
·t
(
P, f
);
(6.18)
∆
X =
s
x
·t
(
P, f
)
.
(6.19)
Значения
s
x
и ∆
X
, найденные при
n
j
= 1, являются характеристиками
воспроизводимости аналитического метода, если
х
– концентрация
(количество), а
у
есть функция
х
.
Обычно результаты статистической обработки по методу наименьших
квадратов сводят в таблицу (табл. 7).
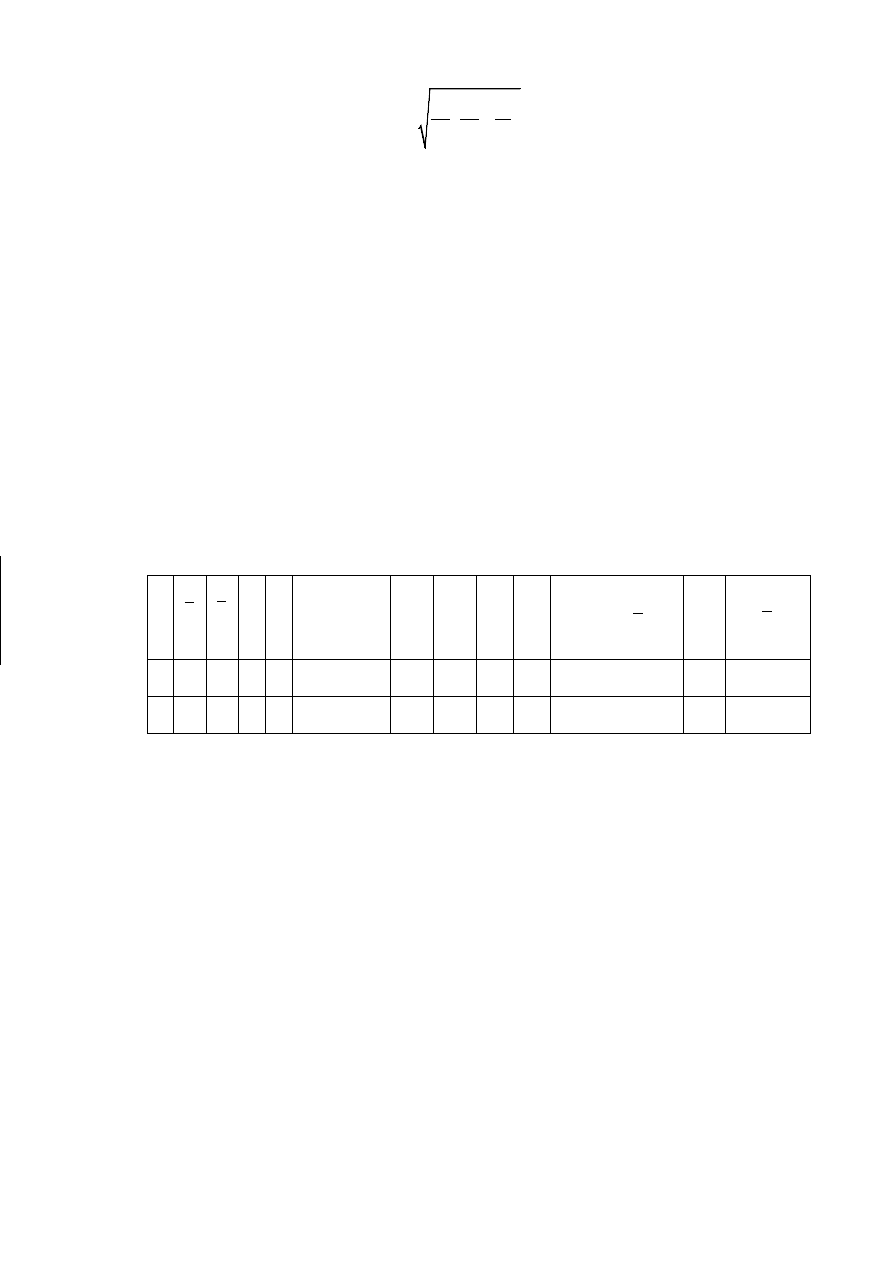
Таблица 7
−
Результаты статистической обработки экспериментальных
данных, полученных при изучении линейной зависимости у = bx + a
f
x
y
b a
t
(
P; f
)
при
P =
95 %
b
∆
a
∆
s
2
0
r s
x
при
n
j
=
1,
y
j
=
y
∆
X
100
⋅
∆
X
––––––,
x
%
1 2 3 4 5
6
7 8 9 10
11
12
13
Примечание 6.1
.
Если целью экспериментальной работы являлось
определение констант
b
и
a
, графы 11, 12 и 13 табл. 7 не заполняются.
Примечание 6.2. Если
y = b·
lg
x + a
, вычисления, описанные в
разделе 6, выполняют с учетом примечаний 1.2 и 2.2.
Примечание 6.3. Сравнение дисперсий
2
0
s
, полученных в разных
условиях для двух линейных зависимостей, может быть проведено, как
указано в разделе 3 (см. выражения (3.4), (3.5) и (3.5 а)).
7. Расчет неопределенности функции нескольких случайных
переменных
Описанные в разделах 1 – 6 настоящей общей фармакопейной статьи
расчеты доверительных интервалов результатов методик анализа применимы
лишь в том случае, если измеряемая величина (концентрация, содержание и
т.д.) является функцией только одной случайной переменной. Такая ситуация
обычно возникает при использовании прямых методов анализа (титрование,
определение сульфатной золы, тяжелых металлов и т.д.). Однако большинство
Предыдущая < | 312 | > Следующая | Главная | pharma-14@mail.ru | pharmacopeia.ru